Published at 2021-11-06 14:58
Author:zhixy
View:4088
历史上最早得到正态分布的功劳应该归于法国数学家亚伯拉罕·棣莫弗(Abraham de Moivre),后来另一位法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)又对棣莫弗的结果进行了完善。与拉普拉斯同时期的德国大数学家约翰·卡尔·弗里德里希·高斯(Johann Carl Friedrich Gauss)在研究测量误差时,从另一个角度也推导出了正态分布,并率先将其应用于天文学研究,高斯的这项工作对后世的影响极大,使得正态分布同时有了“高斯分布”的名称。那么,棣莫弗又是如何在280多年前(1733年)得到正态分布的呢?故事还得从二项分布说起。
设有个服从
两点分布的随机变量
,同时令
的两个对立的结果分别为
和
,沿用掷硬币的例子,这里相当于掷
个同等质量的硬币,然后正面向上的记
分,反面向上的记
分。那么总分数
。假如这样的掷硬币过程重复多次,
的平均会有多少分呢?根据数学期望的定义,
。因为表示的是第
个掷出的硬币是正面或反面,所以
实际上也就是正面比反面多的个数。类似地,还可以得到
的方差,
。根据上文中关于二项分布的讨论,是服从二项分布的,而且不难看出
只能取偶数值,因为在掷出的
个硬币中,正面比反面多的个数只能是偶数。所以,根据二项分布的概率公式有
的概率为
下面一个重要的公式——斯特林公式就该登场了:,代入上式有
当式,上式中
,所以可得
,调整一下形式有
这与正态分布的概率密度公式
已经非常接近了,其中均值,方差
,分别等于
的期望
和方差
。惟一的差别是常数项的分子为
,而正态分布的概率密度公式的相应因子为
。这一点差异恰恰说明了上面我们已经提到的事实,即
取奇数值的概率为0,所以
取偶数值的概率是所期望的
倍。
当随机变量服从正态分布,即
时,
的一个函数
的概率密度函数,根据随机变量函数的概率密度的一般求法,有
所以,服从
的正态分布,即标准正态分布。
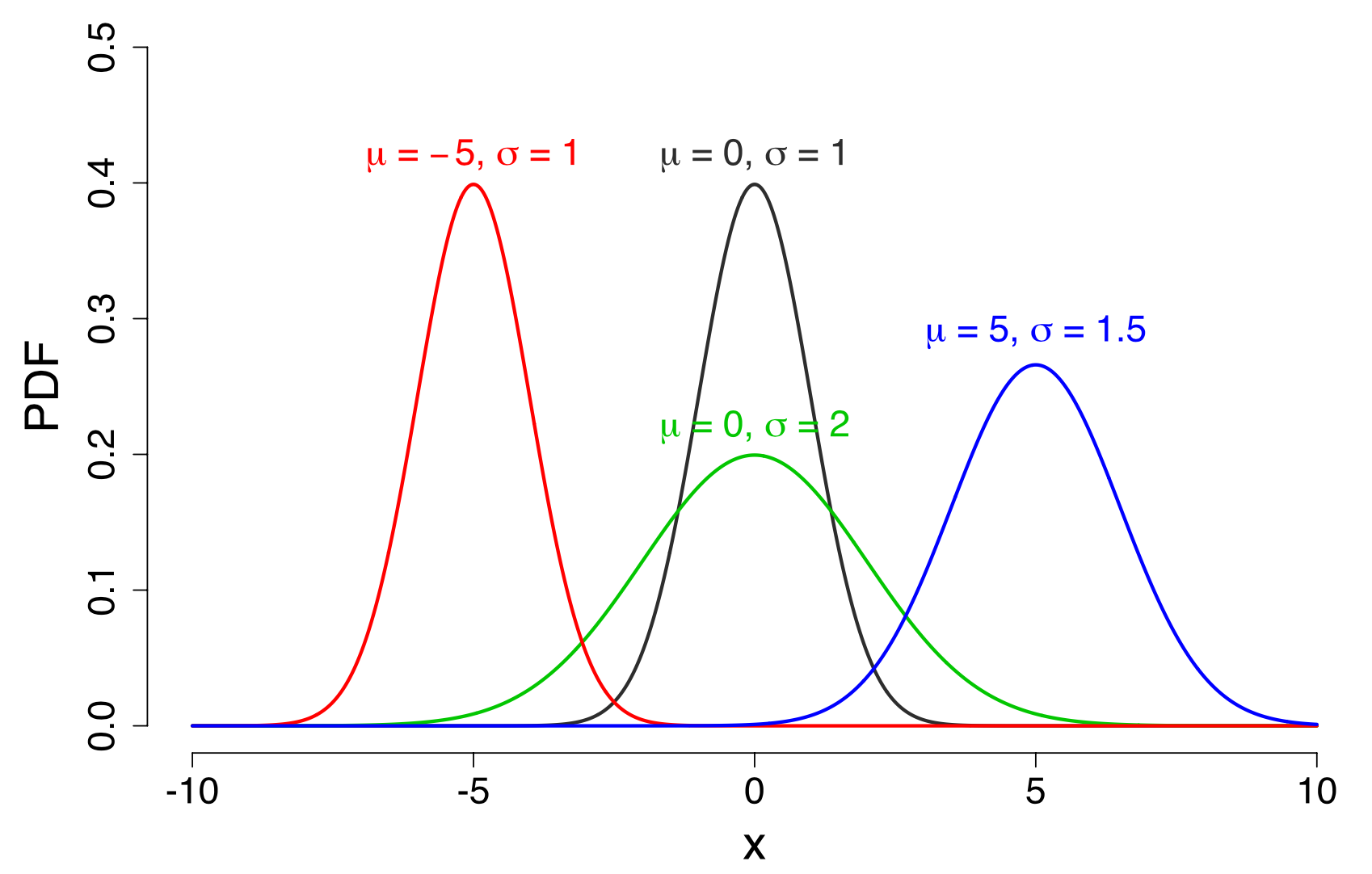
卡方分布是三大抽样分布之一,总是在假设检验中出现。如果随机变量服从自由度为
的卡方分布,那么
具有概率密度函数
记作。卡方分布中自由度
对分布的形状影响极大。在统计学中,很多假设检验的检验统计量在原假设下服从卡方分布,这类假设检验尤其适用于分类数据。卡方检验是一种非参数检验,也就是说它对数据来源的总体分布不做任何假设(但相比于参数检验,卡方检验的统计效果差)。
卡方分布是由相互独立且均服从正态分布的随机变量的平方之和构成的。最简单的情形是这样的,假设随机变量服从标准正态分布,即
,那么
服从自由度为
的卡方分布,即
。为证明这一重要结果,先令
,那么随机变量
的概率分布函数可写为
代入的概率分布函数,并求导
所以随机变量服从自由度为
的卡方分布,并且数学期望为
,方差为
。从一个服从标准正态分布随机变量的平方,推广到
个标准正态分布随机变量的平方之和,对应的卡方分布会在自由度上由
变为
。设一个正整数
,从
到
是
个独立且同为标准正态分布的随机变量,那么就有
,服从自由度为
的卡方分布,即
。卡方分布具有可加性,即
。所以假设有
,
个相互独立且均服从卡方分布的随机变量,那么它们的和
服从自由度为
的卡方分布。
卡方分布要求构成它的随机变量服从标准正态分布,如果这些随机变量服从一般的正态分布(均值不同、方差相同),即,那么此时
服从自由度为
的非中心卡方分布,有概率密度函数
其中称为非中心参数,有数学期望
和方差
。
从同一正态总体中抽取的相互独立的
个随机变量
,它们的联合分布仍为正态分布,且有概率密度函数
,这里指数部分出现的也就是自由度为
的
。
分布是第二个重要的抽样分布。在假设检验中,来自某正态总体
的一组样本
其平均数的
的函数
,统计量
服从标准正态分布。因为每次抽出一组样本,会得到可能有变化的
,所以
也是一个随机变量,而且有均值
和标准差
(又称标准误)。根据上述标准正态分布的推导过程,不难理解
。有了这个结论就可以完成假设检验的统计推断。但是如果正态总体的标准差
未知,统计量
就不存在了。实践中我们会用样本标准差来代替(估计)总体标准差,构造出来的新的统计量,用
表示,即
。此时的
不再服从标准正态分布。
如何得到统计量的概率密度函数?我们得从
说起。
假设有随机变量,产生一组样本
,因为
,所以
服从自由度为
的
分布。将
进行分解,得到
,其中由于是一个常数,所以
,且
,因此
,所以
现在请仔细观察上式,等号最左边,最右边第二项,由于
,所以
。根据卡方分布的可加性,可知等号右边第一项
(该结论也用于方差的区间估计)。
现在我们再回到统计量的定义,并作变形,得到
令,
,所以
,其中
和
分别所代表的是随机变量
和
。因此,
统计量的概率密度可以利用标准正态分布和卡方分布的概率密度推导出来,首先来看分母部分,令
。
其中为自由度为
的卡方分布的概率密度公式。利用积分上限函数的求导公式对
求导,得
的密度函数
。连同
的密度
函数,导入随机变量商密度函数的一般公式,得

将替换为常用的随机变量符号
,得
,该式即是自由度为的
分布的概率密度函数。
所以在假设检验中,当总体分布的方差未知,用样本方差
来估计,所得的统计量
服从自由度
的
分布。
由表达式可知,
分布可以理解为由两个随机变量
和
构成的函数
的概率分布。这里假如
,那么相应的
分布则变为自由度为
的非中心
分布,有概率密度函数
其中称为非中心参数,有数学期望
和方差
。
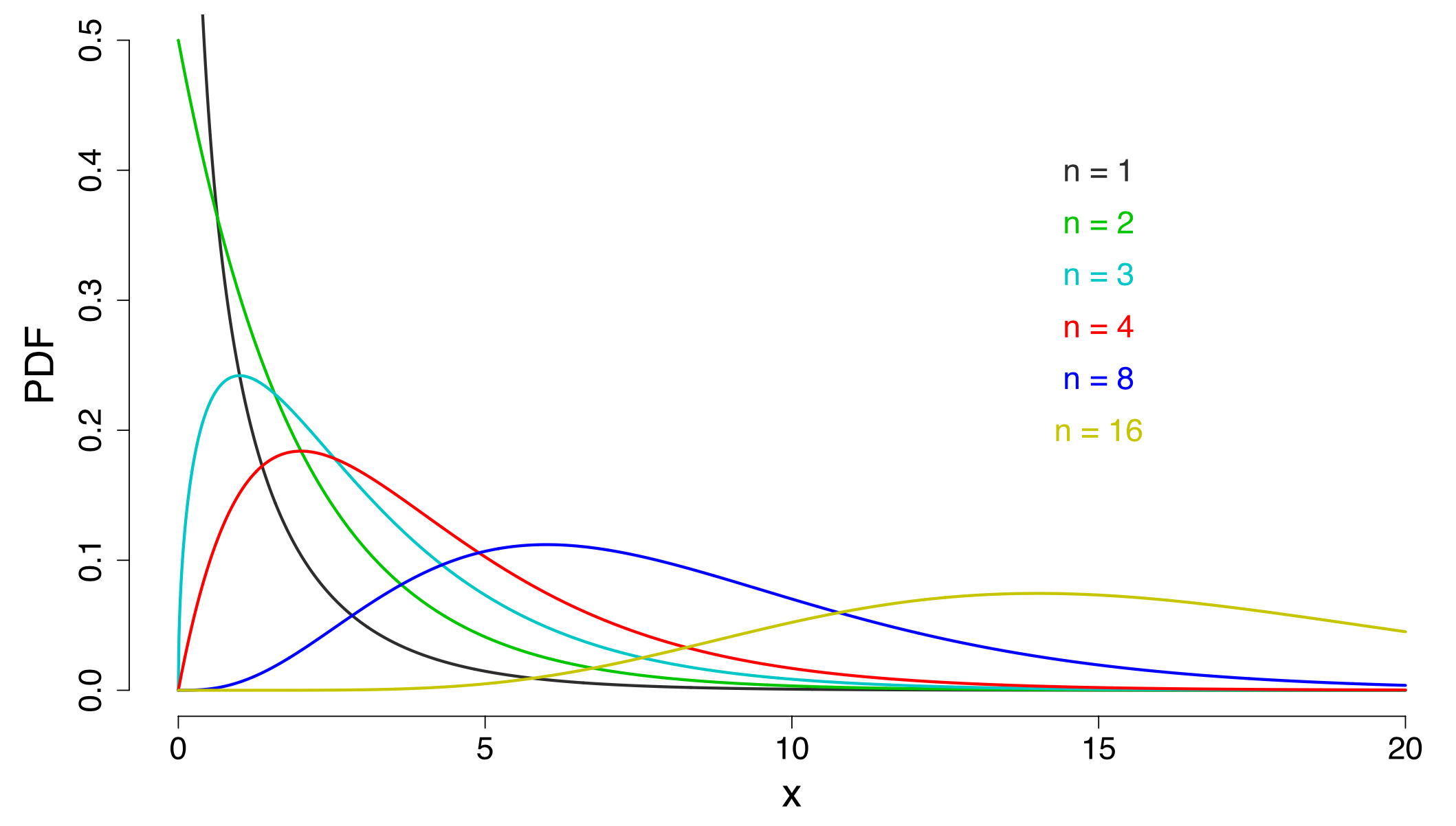
假设检验中的检验和
检验是关于样本平均数的检验,而对样本方差的检验需要用到卡方分布或
分布。当比较来自两个总体的样本方差之间是否存在显著差异时,会将两样本方差作比值,然后与
比较。假设有两个正态总体
和
分别产生两组样本(容量分别为
和
),样本方差分别为
和
,那么
且已知和
,所以
实际上表示的是两个随机变量
和
分别除以各自的自由度后再相除所得的随机变量。首先令
,
其中为自由度为
的卡方分布的概率密度公式。利用积分上限函数的求导公式对
求导,得
的密度函数为
。同理可得
的密度函数为
。导入随机变量商密度函数的一般公式,得

同样地,用常用的随机变量符号替换,得
,即自由度为和
的
分布的概率密度函数。
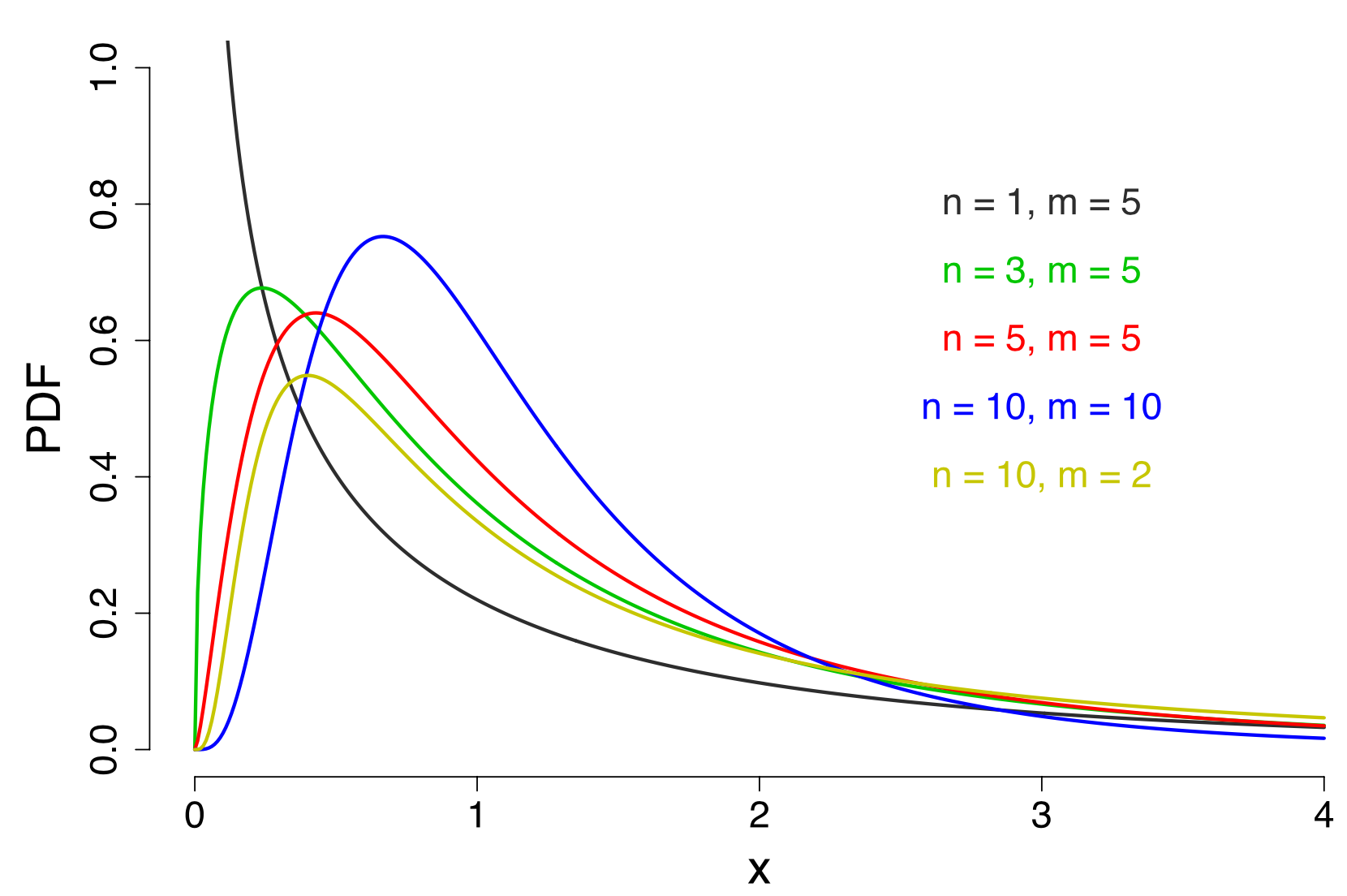
与卡方分布和分布类似,
分布也有非中心的
分布。在构成
分布的两个服从卡方分布的随机变量,只要让出现在分子位置上的随机变量服从非中心卡方分布,
分布就实现了非中心化。
柯西分布的概率密度函数为
,其中为尺度参数,
为位置参数。当
时的特例称为标准柯西分布。
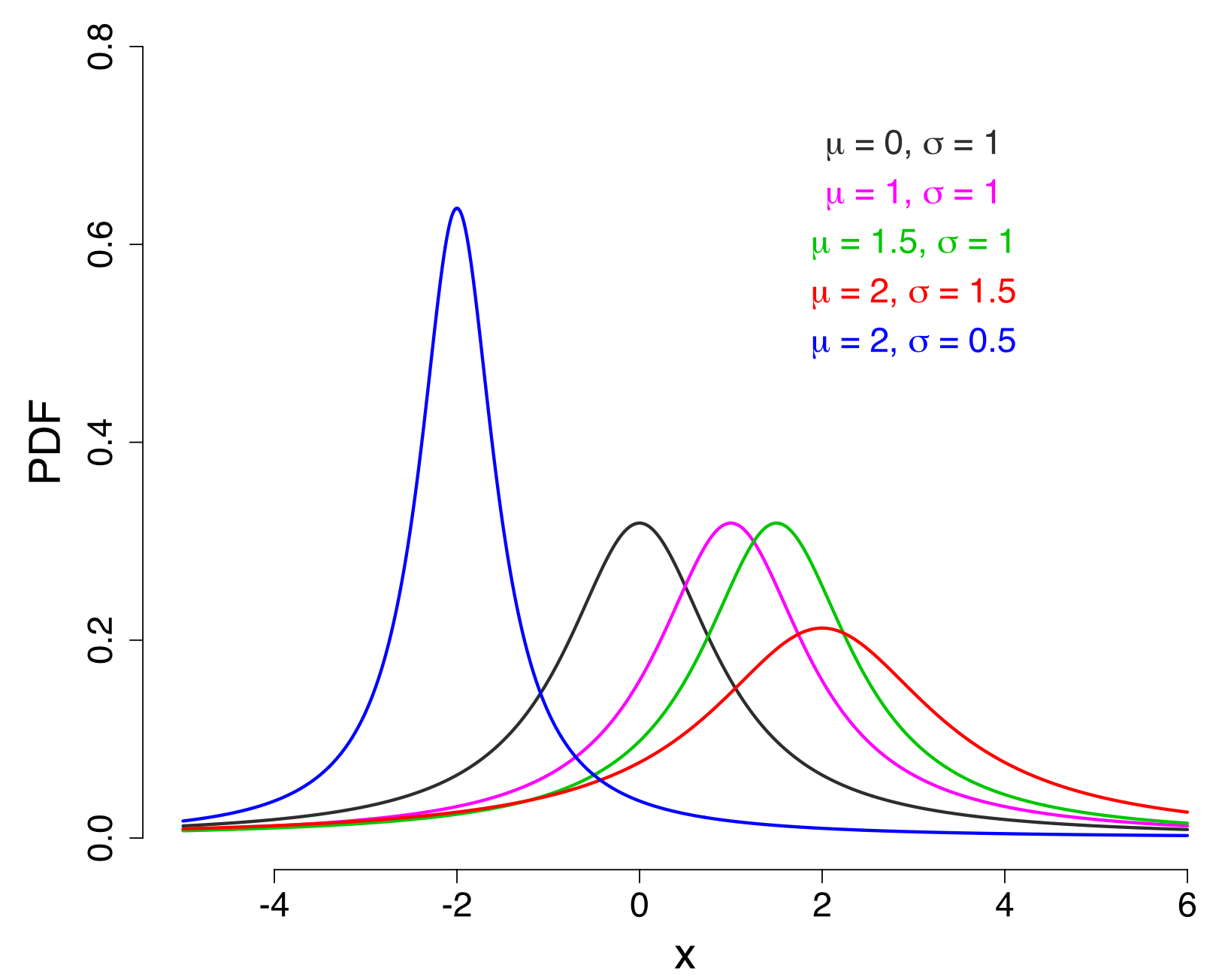
柯西分布是一种非常特殊的概率分布,它的均值和方差不存在,但有中位数和众数,也就是位置参数,下四分位数为
,上四分位数为
。
柯西分布具有可加性,即如果有和
,那么
。
两个标准正态分布之比服从标准柯西分布,标准柯西分布的倒数仍是标准柯西分布。
标准柯西分布还等同于自由度为的
分布,而一般的柯西分布等同于自由度为
的非标准化的
分布。
柯西分布概率密度函数的雏形最早出现于数学家费马的著作(17世纪中叶),后来陆续被牛顿、莱布尼茨、惠更斯、盖多·格兰迪和玛利亚·加塔娜·阿涅西研究过。到了19世纪,这种曲线了一个特殊的名称——“阿涅西箕舌线”。1824年之间柯西密度曲线并没有作为一种可能的误差分布出现,然而当它用于误差研究时,却是作为其他一般定理的反例出现的。而且被发现了两次,更有趣的是两位发现者寻找它的动机不同,并以两种不同的方式解释了它的重要性。1824年,泊松发文首次注意到了具有标准柯西密度函数的概率分布,并发现它具有一些相当特殊的性质,并且可以产生一些统计学中普遍接受的结果的反例。泊松的论文旨在澄清并略微扩展拉普拉斯在最小二乘法方面的一些工作。1810-1811年,拉普拉斯通过证明我们现在所称的中心极限定理,为勒让德的最小二乘原理提供了一个大样本的理由,并指出,由于最小二乘法是处理正态分布误差的最佳方法,它对任何误差分布都是最佳的,至少对大样本是如此。当时,拉普拉斯忽略了任何正则性条件(用于限定定理使用范围的限定条件),只假设误差分布是对称的。在综述拉普拉斯的工作室,泊松呼吁应当特别注意密度函数。他指出,如果对误差分布为
的多个观测值取平均值,则随着观测值数量的增加,平均误差不会收敛到零或任何其他数字,而是具有相同的分布,无论观测值数量有多大。虽然泊松清楚地意识到在这一特殊情况下可能出现的困难,但他并不十分重视它。
柯西与柯西分布第一次邂逅源自一场发生在1853年的数学争端,挑起争端的是不太出名的数学家伊瑞·朱尔斯·比内梅(拉普拉斯的忠实信徒),他发文称Cauchy在1835年提出的插值方法与概率论存在冲突,因为它通常不会给出与最小二乘法相同的结果。随后,柯西连发七文反击了比内梅的“挑衅”,当然期间比内梅也做了四次回应。争论最终甚至演变成两人开始互相伤害。柯西坚持认为,虽然这两种方法是不同的,每种方法都有其优点和缺点。但是他认为概率论并没有赋予最小二乘法独特的优势。为了证明他的观点,柯西用特征函数作为工具发现,尽管最小二乘法为正态分布误差提供了“最可能”的值,但在其他情况下却没有。柯西给出了密度函数作为“其他情况”的例子。柯西论证的力量在于,只有正态分布的最小二乘法才是最好的;与攻击拉普拉斯的证明相比,他更关心的是对特征函数的严格处理和捍卫他的插值方案。在比内梅的回应中,提到了泊松之前工作,之所以忽视柯西密度是因为在实践中不会出现。最后通过拉着拉格朗日、高斯、拉普拉斯和贝塞尔一起为最小二乘法背书。这场争论虽然短暂,但很活跃。柯西为他差值法辩护,通过运用他强大的分析能力证明最小二乘法在线性估计中不具有自然的垄断性。另一方面,比内梅则站在拉普拉斯权威所捍卫的立场上进行辩论,他渴望不让正则性条件干扰他所认为的实际真理。
很难说是谁最后赢的了这场数学争端。他们在不同的前提下争论,两者都是正确的。讽刺的是,在争论的最后一篇文章中,柯西严格证明了中心极限定理,并承诺在未来的文章中探讨其统计意义。但柯西再也没有回到这个话题上来,也许是因为他看到自己正在危险的滑向对手的阵营。
正态分布之于随机变量概率分布,就像夜空中最闪亮的星,最常被用来描述许多学科的数据中出现的随机变化。然而许多测量结果显示出或多或少的偏态分布。当平均值低、方差大、取值不能为负时,偏态分布尤其常见,例如,物种丰富度、传染病潜伏期的长短以及地壳中矿产资源的分布。这种偏态分布通常符合对数正态分布。设是取正值的连续随机变量,如果
服从正态分布,则
服从对数正态分布,有概率密度函数
,数学期望和方差
。
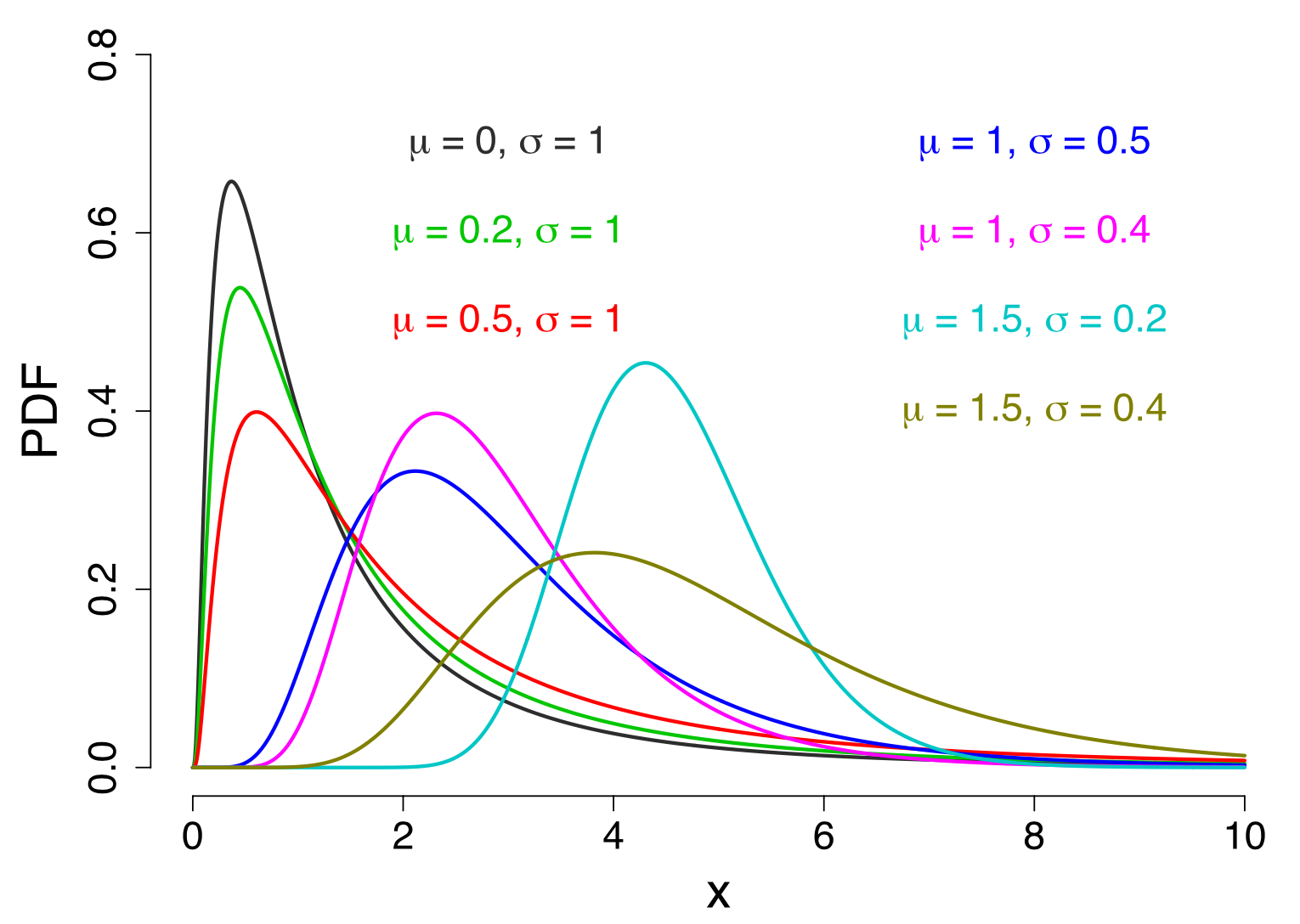
所以正态分布经指数变换后即为对数正态分布;对数正态分布经对数变换后即为正态分布。此外当,
是正实数,
是参数为
的对数正态分布,则
仍是对数正态分布,参数为
。简单来说,对数正态分布之积还是对数正态分布。我们知道正态分布之和仍是正态分布,实际上两者之间是有逻辑关系的。对数正态分布相乘等同于其幂指数相加,而服从对数正态分布的随机变量,如果写成自然底数的次幂形式,那么幂指数服从正态分布。因此对数正态分布之积等同于正态分布之和。
正态分布与对数正态分布之间的关系,与随机变量变异的可加性和可乘性有关。随机变量不同取值的变异性是用方差或标准差来衡量的。我们再观察一下方差的公式,其意义实际上是每个
到均值
的距离平方的平均值。也就是说每个
,
表示距离(也是一个随机变量),所以这里随机变量的变异性是通过加/减法实现的,即随机变量变异具有可加性。如果随机变量的变异性是通过乘/除法实现的,比如
,那么该随机变量的变异则具有可乘性。变异的可加性与可乘性分别导致正态分布和对数正态分布,而正态分布与对数正态分布又分别对应算术平均数和几何平均数。
